Aprende cómo aplicar la regla de Ruffini en tus clases

¿Quién fue Bernardino Ruffini?

La regla de Ruffini se refiere a las ideas del físico y matemático italiano Bernardino Ruffini, quien es conocido por sus contribuciones a las matemáticas, particularmente en el campo de la teoría de ecuaciones. Ruffini es famoso por haber demostrado, en gran medida, la imposibilidad de resolver algebraicamente ecuaciones de grado cinco o superior “ecuaciones quínticas” mediante radicales, es decir, usando solo sumas, restas, multiplicaciones, divisiones y raíces. Este trabajo es un precursor de la teoría de Galois, que más tarde formalizó esta imposibilidad. 

¿Qué aportó a las matemáticas?

Este autor trabajó en el problema de la resolubilidad por radicales, que se refiere a si es posible encontrar soluciones exactas para ecuaciones polinómicas de cualquier grado utilizando solo operaciones algebraicas elementales (como sumas, restas, multiplicaciones, divisiones y extracción de raíces). Para ecuaciones de grado cuatro o inferior, como las cuadráticas, cúbicas y cuárticas, ya se conocían métodos de solución exacta. Sin embargo, para las ecuaciones de grado cinco o superior, Ruffini propuso que no era posible obtener una solución exacta mediante estos métodos. 

Ruffini fue uno de los primeros en proponer formalmente que no todas las ecuaciones polinómicas de grado mayor a cuatro pueden resolverse mediante radicales. Aunque su demostración no fue completamente rigurosa desde el punto de vista moderno, sentó las bases para que otros matemáticos, como Niels Abel y Évariste Galois, consolidaran la teoría. También, identificó muchos conceptos que más tarde serían formalizados en la teoría de Galois, un área clave en el álgebra abstracta que estudia las simetrías de las raíces de las ecuaciones polinómicas y establece criterios precisos sobre cuándo una ecuación es resoluble por radicales. 

De esta manera se puede considerar que este autor abrió el camino para una mejor comprensión de la estructura de las ecuaciones polinómicas y de cuándo pueden resolverse algebraicamente. Su trabajo fue un gran avance hacia la matemática moderna, y aunque en su tiempo no fue completamente reconocido, más tarde fue visto como fundamental para el desarrollo del álgebra abstracta y la teoría de ecuaciones.

A modo de ejemplo vamos a dividir el polinomio

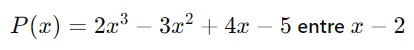
Aprende paso a paso la regla de Ruffini

Paso 1: coeficientes del polinomio 

Primero, identificamos los coeficientes del polinomio En este caso, los coeficientes de son:  

Paso 2: Raíz del binomio divisor 

El divisor es   

Paso 3: Aplicación del método de Ruffini 

Ahora organizamos los coeficientes en una tabla y empezamos el procedimiento de la Regla de Ruffini. 

1. Escribimos los coeficientes del polinomio 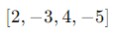en una fila. 

2. Dejamos un espacio debajo para escribir los valores intermedios. 

3. El primer coeficiente (2) se baja directamente al resultado. 

4. Luego multiplicamos este valor por 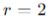y lo sumamos al siguiente coeficiente (-3). Así, seguimos el proceso. 

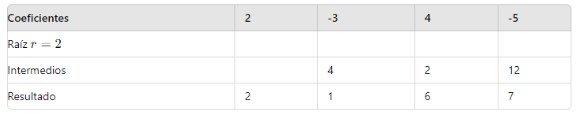
Paso 4: interpretación de los resultados 

El último número de la fila inferior es el resto de la división, y los números anteriores son los coeficientes del cociente. 

• Cociente:   

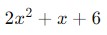
• Resto: 7 

Paso 5: expresión del resultado 

La división de es:  

Esto significa que el cociente es   

De esta manera podemos identificar como la Regla de Ruffini nos permite realizar divisiones de polinomios de forma rápida cuando el divisor es un binomio de la forma x−r, proporcionando el cociente y el resto sin necesidad de realizar la división larga convencional. En el aula, esta teoría puede aplicarse de diversas maneras para ayudar a los estudiantes a comprender no solo la técnica, sino también su contexto y utilidad en matemáticas más avanzadas.

La regla de Ruffini en el aula

Antes de que los estudiantes utilicen la Regla de Ruffini, es importante explicar la teoría detrás de la división de polinomios y cómo se relaciona con encontrar raíces. Puedes comenzar con ejemplos sencillos de división de polinomios usando el método tradicional para mostrar por qué Ruffini es más eficiente en ciertos casos, como al dividir por binomios de la forma x−r. Una vez que los estudiantes entiendan el contexto, introduce la Regla de Ruffini paso a paso: 

• Presenta un polinomio sencillo y divide entre un binomio como x−1 o x+2. 

• Enséñales a organizar los coeficientes del polinomio en la tabla de Ruffini y cómo llevar a cabo el proceso de multiplicación y suma. 

Una vez que se ha explicado el método, los estudiantes pueden practicar con ejemplos guiados. Proporcionales polinomios sencillos para que trabajen en pares o grupos pequeños. Luego, revisa las soluciones en conjunto, reforzando el proceso y resolviendo dudas. Muestra a los estudiantes cómo la Regla de Ruffini es útil para encontrar raíces de polinomios o para resolver ecuaciones. Al conectar el método con problemas matemáticos más grandes, los estudiantes verán su utilidad en lugar de solo memorizar un procedimiento. T

También, incorpora el uso de calculadoras gráficas o software matemático (como GeoGebra o Desmos) para que los estudiantes puedan visualizar el polinomio y cómo se comportan sus raíces. Estas herramientas pueden ayudarles a entender mejor cómo la Regla de Ruffini se conecta con la gráfica de una función polinómica. 

Es así como puedes llevar la regla de Ruffini al aula a través de una combinación de explicación teórica, prácticas guiadas, aplicaciones tecnológicas, y actividades colaborativas, creando una experiencia de aprendizaje activa y comprensible.